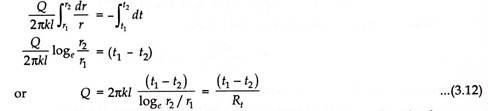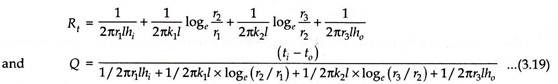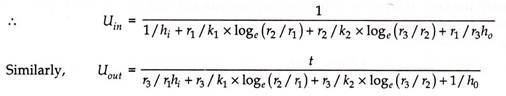Conduction of Heat through Cylindrical Wall | Thermal Engineering

In this article we will discuss about the procedure for conduction of heat through a cylindrical wall and multi-layer cylindrical wall.

Conduction of Heat through a Cylindrical Wall:

Cylindrical metal tubes constitute an essential element of power stations, oil refineries and most process industries. The boilers have tubes in them, the condensers contain bank of tubes, the heat exchangers are tubular and all these units are connected by tubes. Evidently then the radial heat transfer rate through a tube or any insulation which may surround it is quite important.

Consider heat conduction through a cylindrical tube of inner radius r₁, outer radius r₂ and length l. The inside and outside surfaces of the tube are at constant temperatures t₁ and t₂ and thermal conductivity k of the tube material is constant within the given temperature range. If both ends are perfectly insulated, the heat flow is limited to radial direction only. Further if temperature t₁ at the inner surface is greater than temperature t₂ at the outer surface, the heat flows radially outwards.

Consider an infinitesimally thin cylindrical element at radius r. Let thickness of this elementary ring be dr and the change of temperature across it be dt. Then invoking Fourier law of heat conduction

Separating the variables and integrating within the prescribed boundary conditions, we obtain-

Evidently for conduction in a hollow cylinder, the thermal resistance takes the form

The expression for steady state temperature distribution in a cylindrical walk can be set up by integrating the Fourier rate equation between the limits-

(i) r = r₁ where the temperature is stated to be t₁

(ii) r = r where the temperature is to be worked out

(iii) Quite often it is considered advantageous to write the heat flow equation through a cylinder in the same form as that for heat flow through a plane wall. Then thickness δ will be equal to (r₂ -r₁) and the area A will be an equivalent area A_m. Thus

 

Comparing equations 3.11 and 3.12,

where A₁ and A₂ are the inner and outer surface areas of the cylindrical tube. The equivalent area A_m is called the logarithmic mean area of the tube. Further,

Obviously, logarithmic mean radius of the cylindrical tube is-

Example 1:

A cylindrical cement tube of radii 0.05 cm and 1.0 cm has a wire embedded into it along its axis. To maintain a steady temperature difference of 120°C between the inner and outer surfaces, a current of 5 ampere is made to flow in the wire. Make calculations for the amount of heat generated per metre length and the thermal conductivity of cement.

Take resistance of wire equal to 0.1 ohm per cm of length.

Solution:

Resistance of wire, R = 0.1 Ω per cm length

= 10 Ω per m length

Heat generated = I² R = 5² × 10 = 250 W/m length

Under steady state conditions, the heat generated equals the heat transfer through the cylindrical element.

Conduction of Heat through a Multi-Layer Cylindrical Wall:

Multi-layer cylindrical walls are frequently employed to reduce heat losses from metallic pipes meant for handling a hot fluid. The pipe is generally wrapped in one or more layers of heat insulation, e.g., a steam pipe used for conveying high pressure steam in a steam power plant may have cylindrical metal wall, a layer of insulating material and then a layer of protecting plaster. The arrangement is called lagging of the pipe system.

Fig. 3.21 shows conduction of heat through a composite cylindrical wall having three layers of different materials. There is a perfect contact between the layers and so an equal interface temperature for any two neighbouring layers.

For steady state conduction, the heat flow through each layer is same and it can be described by the following set of equations:

These equations help to determine the temperature difference for each layer of the composite cylinder, i.e.,

Thus the heat flow rate through a composite cylindrical wall is-

The quantity in the denominator is the sum of the thermal resistance of the different layers comprising the composite cylinder.

When the above relation is extended to a hollow composite cylinder of n-concentric shells enveloping each other, the heat flow rate is given by-

If the internal and external heat transfer coefficients for the composite cylinder depicted in Fig. 3.22 are h_i and h_o respectively, then the total thermal resistance to heat flow would be-

Introducing the concept of overall heat transfer coefficient U, the heat flow rate can be written as:

Q = UA (t_i – t₀).

Since the flow area varies for a cylindrical tube, it becomes necessary to specify the area on which U is based. Thus depending upon whether the inner or outer area is specified, two different values are defined for U, i.e.,

Example 2:

A steam pipe 10 cm outside diameter is covered with two layers of insulation, each having a thickness of 2.5 cm. The average thermal conductivity of one material is 3 times that of other and the surface temperatures of the insulated steam pipe are fixed. Examine the position of better insulating layer relative to the steam pipe if heat dissipation from steam is to be minimum. What % age saving in heat dissipation results from that arrangement?

Solution:

The geometrical dimensions of the lagged steam pipe are:

r₁ = 5 cm; r₂ = 7, 5 cm; r₃ = 10 cm

Let k and 3k be the thermal conductivities of the two insulating materials. Obviously the material with low thermal conductivity is a better insulator.

(i) Better insulator (material with low thermal conductivity) is placed inside, i.e., next to the steam pipe.

(ii) Better insulator is outside

Obviously the heat dissipation is small when the material with low thermal conductivity is placed next to the steam pipe

Saving in heat dissipation

= 4.7303 – 3.99/3.99 × 100 = 18.55%