In this article we will discuss about:- 1. Heat Conduction through a Plane Wall 2. Heat Conduction through a Composite Wall 3. Effect of Variable Conductivity.
Heat Conduction through a Plane Wall:
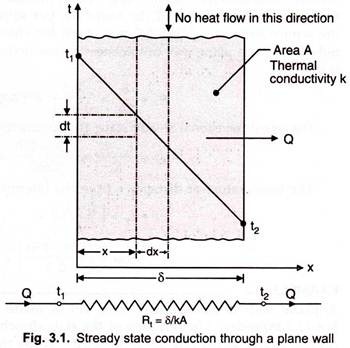
Consider one-dimensional heat conduction through a homogeneous, isotropic wall of thickness 8 with constant thermal conductivity k and constant cross-sectional area A. The wall is insulated on its lateral faces and constant but different temperatures t1 and f2 are maintained at its boundary surfaces. Obviously temperature varies only in the direction normal to the wall and the temperature potential causes heat transfer in the positive x-direction.
The attention is focused on an elementary strip of thickness dx located at a distance x from the reference plane. The temperature difference across the strip is dt and obviously the temperature gradient is dt/dx. Since Q is constant in a steady state, the terms of the Fourier rate equations Q = – kA (dt/dx) may be separated and integrated directly between the limits t = t1 at x = 0 and t = t2 at x = δ. Thus-
The expression for steady state temperature distribution can be set up by integrating the Fourier rate equation between the limits:
(i) x = 0 where the temperature is stated to be t1.
(ii) x = x where the temperature is to be worked out
where Rt = δ/kA is the thermal resistance to heat flow. Equivalent thermal circuit for heat flow through a plane wall has been included in Fig. 3.1.
ADVERTISEMENTS:
Example 1:
The interior of an oven is maintained at a temperature of 850°C by means of a suitable control apparatus. The oven walls are 500 mm thick and are fabricated from a material of thermal conductivity 0.3 W/m-deg. For an outside wall temperature of 250°C, workout the resistance to heat flow and the heat flow per square metre of wall surface. Also calculate the temperature at a point 200 mm from the interior side.
Solution:
ADVERTISEMENTS:
For a plane wall of thickness δ, conductivity k and area A, the thermal resistance Rt is given by-
Example 2:
A plane slab of thickness 8 = 60 cm is made of a material of thermal conductivity k = 17.5 W/m-deg. The left side of the slab absorbs a net amount of radiant energy from a radiant source at the rate q = 530 watt/m2. If the right hand face of the slab is at a constant temperature t2 = 38°C, set up an expression for temperature distribution within the slab as a function of relevant space co-ordinates. Therefrom work out the temperature at the mid- plane of the slab and the maximum temperature within the slab. It may be presumed that the temperature distribution is steady and there is no heat generation.
ADVERTISEMENTS:
Solution:
Under stipulations of steady state and no heat generation, the energy absorbed from the radiant source equals the rate at which it is conducted through the slab.
This also represents the maximum temperature within the slab. From the expression for steady state temperature distribution,
Heat Conduction through a Composite Wall:
A composite wall refers to a wall of a several heterogeneous layers, e.g., walls of dwelling houses where bricks are given a layer of plaster on either side. Likewise walls of furnaces, boilers and other heat exchange devices consist of several layers; a layer for mechanical strength or for high temperature characteristics (fire brick), a layer of low thermal conductivity material to restrict the flow of heat (insulating brick) and another layer for structural requirements for good appearance (ordinary brick).
Fig. 3.6 shows one such composite wall having three layers of different materials tightly fitted to one another. The layers have thicknesses δ1, δ2, δ3 and their thermal conductivities correspond to the average temperature conditions. The surface temperature of the wall are t1 and t4 and the temperatures at the interfaces are t2 and t3.
Under steady state conditions, heat flow does not vary across the wall, i.e., it is same for every layer. Thus-
Distributing of temperature in a plane multilayer wall is represented by a polygonal line (Fig. 3.6).
When the above analysis is extended to an n-layer composite wall, one obtains:
where is sum of the thermal resistances of different layers comprising the composite wall.
Analysis of the composite wall assumes that there is a perfect contact between layers and no temperature drop occurs across the interface between materials.
Example 3:
An exterior wall of a house may be approximated by 10 cm layer of common brick (k = 0.75 W/m-deg) followed by 4 cm layer of gypsum plaster (k = 0.5 W/m-deg). What thickness of loosely packed rock wool insulation (k = 0.065 W/m-deg) should be added to reduce the heat loss or gain through the wall by 75%?
Solution:
Thermal resistance for a plane wall of thickness δ, area A and thermal conductivity k is prescribed by the relation Rt = δ/kA. Considering unit area of wall perpendicular to heat flow direction,
Example 4:
The walls of house in cold region comprise three layers
15 cm outer brick work (k = 0.75 W/m-deg)
1.25 cm inner wooden paneling (k = 0.2 W/m-deg)
7.5 cm intermediate layer of insulating material
The insulation layer is stated to offer resistance twice the thermal resistance of brick work. If the inside and outside temperatures of the composite wall are 20°C and -15°C respectively, determine the rate of heat loss per unit area of the wall and the thermal conductivity of the insulating material.
Solution:
Thermal resistance for a plane wall of thickness δ, area A and thermal conductivity k is prescribed by the relation Rt = δ/kA
Effect of Variable Conductivity:
For most materials, the dependence of thermal conductivity on temperature is almost linear
k = k0 (1 + βt) … (3.29)
where k0 is the thermal conductivity at zero degree centigrade temperature and β is a constant whose value depends upon the material. This constant may be positive or negative depending upon whether thermal conductivity increases or decreases with temperature. The coefficient β is usually positive for non-metals and insulation materials (exceptions are magnesite bricks) and negative for metallic conductors (exceptions are aluminium and certain non-ferrous alloys).
With variable thermal conductivity, Fourier law of heat conduction through a plane wall can be expressed as-
Separating the variables and integrating within the limits t = t1 at x = 0 and t = t2 at x = δ
The quantity km = k0 (1 + β/2 (t1 + t2) represents the mean thermal conductivity evaluated at the arithmetic mean temperatures 1/2 (t1 + t2).
Temperature Variation:
Fourier law of heat induction through a plane wall is
Q = – k A dt/dx; Q/A = – (k dt/dx)
For steady state heat conduction in the infinite wall, Q/A is constant and so has to be the parameter (k dt/dx). Obviously then, the temperature variation in the wall is governed by the condition that parameter (k dt/dx) is constant.
Case I β = 0: We have,
k = k0 (1 + βt) = k0 = constant
The thermal conductivity does not vary with temperature and equals the constant value k0. Accordingly for the parameter (k dt/dx) to be constant, the term dt/dx must be constant. Therefore, the slope of temperature curve is constant and the temperature profile is linear.
Case II P > 0: We have,
k = k0 (1 + βt); i.e., k0 ∝ t
The thermal conductivity of the wall material is directly proportional to temperature; k increases with increasing temperature or decreases with decreasing temperature. Since the temperature decreases in x-direction, the thermal conductivity would also decrease. Accordingly to maintain the parameter (k dt/dx) constant, the term dt/dx must increase. Consequently the value of slope increases from point A and B and that means that the curve should go steeper from A to B. Evidently with positive value of β, the temperature variation curve is of convex nature.
Case III β < 0: We have,
k = k0 (1 – βt), i.e., k0 ∝ 1/t
The thermal conductivity of the wall material is inversely proportional to temperature; k decreases with increasing temperature or increases with decreasing temperature. Since the temperature decreases in x-direction, the thermal conductivity would increase. In order to maintain the parameter (k dt/dx) constant, the term dt/dx must decrease. Consequently the value of the slope of temperature profile decreases. Evidently the temperature profile will be concave for negative value of coefficient β.
Example 5:
The inner and outer surfaces of a furnace wall, 25 cm thick, are at 300°C and 30°C respectively. The thermal conductivity of the wall material varies with temperature and is prescribed by the relation
k = (1.45 + 0.5 x 10-5 t2) kJ/m-hr-deg
where t is the temperature in degree centigrade. Proceed from the basic principles to calculate the heat loss per square metre of the wall surface area.
Solution:
Invoking Fourier’s law of heat conduction,