Harmonics: Definition, Types and Causes | Electrical Engineering

In this article we will discuss about: 1. Definition of Harmonics 2. Harmonic Number (h) 3. Types 4. Causes.

Definition of Harmonics:

Harmonics are sinusoidal voltages or currents having frequencies that are integer multiples of the frequency at which the supply system is designed to operate.

Harmonics as pure tones making up a composite tone in music. A pure tone is a musical sound of a single frequency, and a combination of many pure tones makes up a composite sound. Sound waves are electromagnetic waves travelling through space as a periodic function of time. Can the principle behind pure music tones apply to other functions or quantities that are time dependent?

In the early 1800s, French mathematician, Jean Baptiste Fourier formulated that a periodic non-sinusoidal function of a fundamental frequency f may be expressed as the sum of sinusoidal functions of frequencies which are multiples of the fundamental frequency. In our discussions here, we are mainly concerned with periodic functions of voltage and current due to their importance in the field of power quality. In other applications, the periodic function might refer to radiofrequency transmission, heat flow through a medium, vibrations of a mechanical structure, or the motions of a pendulum in a clock.

A sinusoidal voltage or current function that is dependent on time t may be represented by the following expressions:

Voltage function,

v(t) = V sin (ωt) …(4.1)

Current function,

i(t) = I sin (ωt ± θ) …(4.2)

where, ω = 2πf is known as the angular velocity of the periodic waveform and 0 is the difference in phase angle between the voltage and the current waveforms referred to as a common axis. The sign of phase angle θ is positive if the current leads the voltage and negative if the current lags the voltage.

Figure 4.1 contains voltage and current waveforms expressed by Eqs. (4.1) and (4.2) and which by definition are pure sinusoids.

For the periodic non-sinusoidal waveform shown in Fig. 4.2, the simplified Fourier expression states-

V (t) = V₀ + V₁ sin(ωt) + V₂ sin(2 ωt) + V₃ sin(3 ωt) + … + Vn sin( n ωt) + V_n+1 sin (( n + 1) ωt) +………….. (4.3)

The Fourier expression is an infinite series. In this equation, V₀ represents the constant or the DC component of the waveform.

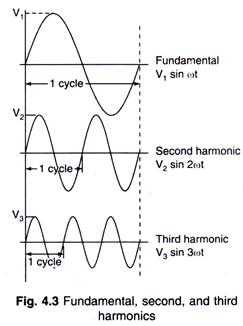
V₁, V₂, V₃, … , V_n are the peak values of the successive terms of the expression. The terms are known as the harmonics of the periodic waveform. The fundamental (or first harmonic) frequency has a frequency of f, the second harmonic has a frequency of 2 x f, the third harmonic has a frequency of 3 x f, and the nth harmonic has a frequency of n x f. If the fundamental frequency is 60 Hz (as in the U.S.), the second harmonic frequency is 120 Hz, and the third harmonic frequency is 180 Hz.

The significance of harmonic frequencies can be seen in Fig. 4.3. The second harmonic undergoes two complete cycles during one cycle of the fundamental frequency, and the third harmonic traverses three complete cycles during one cycle of the fundamental frequency.

V₁, V₂, and V₃ are the peak values of the harmonic components that comprise the composite waveform, which also has a frequency of f.

The ability to express a non-sinusoidal waveform as a sum of sinusoidal waves allows us to use the more common mathematical expressions and formulas to solve power system problems. In order to find the effect of a non-sinusoidal voltage or current on a piece of equipment, we only need to determine the effect of the individual harmonics and then vectorially sum the results to derive the net effect. Figure 4.4 illustrates how individual harmonics that are sinusoidal can be added to form a non-sinusoidal waveform.

The Fourier expression in Eq. (4.3) has been simplified to clarify the concept behind harmonic frequency components in a nonlinear periodic function. For the purist, the following more precise expression is offered. For a periodic voltage wave with fundamental frequency of-

ω = 2πf,

v(t) = V₀ + ∑(a_k cos kωt + b_k sin k ωr) (for k- 1 to ∞)…(4.4)

Where a_k and b_k are the coefficients of the individual harmonic terms or components. Under certain conditions, the cosine or sine terms can vanish, giving us a simpler expression. If the function is an even function, meaning f (-t) = f(t), then the sine terms vanish from the expression. If the function is odd, with f (- t) = – f(t) then the cosine terms disappear.

For our analysis, we will use the simplified expression involving sine terms only. It should be noted that having both sine and cosine terms affects only the displacement angle of the harmonic components and the shape of the nonlinear wave and does not alter the principle behind application of the Fourier series. The coefficients of the harmonic terms of a function-

f(t) contained in Eq. (4.4) are determined by- Coefficient

The coefficients represent the peak values of the individual harmonic frequency terms of the nonlinear periodic function represented by f (t).

Harmonic Number (h):

Harmonic number (h) refers to the individual frequency elements that comprise a composite waveform. For example, h = 3 refers to the third harmonic component with a frequency equal to third times the fundamental frequency. If the fundamental frequency is 60 Hz, then the 3^rd (third) harmonic frequency is 3 x 60, or 180 Hz. The harmonic number 6 is a component with a frequency of 360 Hz.

Dealing with harmonic numbers and not with harmonic frequencies is done for two reasons. The fundamental frequency varies among individual countries and applications. The fundamental frequency in the U.S. is 60 Hz, whereas in Europe and many Asian countries it is 50 Hz. Also, some applications use frequencies other than 50 or 60 Hz; for example, 400 Hz is a common frequency in the aerospace industry, while some AC systems for electric traction use 25 Hz as the frequency.

The inverter part of an AC adjustable speed drive can operate at any frequency between zero and its full rated maximum frequency, and the fundamental frequency then becomes the frequency at which the motor is operating. The use of harmonic numbers allows us to simplify how we express harmonics. The second reason for using harmonic numbers is the simplification realized in performing mathematical operations involving harmonics.

Types of Harmonics:

Odd and Even Order Harmonics:

As their names imply, odd harmonics have odd numbers (e.g., 3, 5, 7, 9, 11), and even harmonics have even numbers (e.g., 2, 4, 6, 8, 10). Harmonic number 1 is assigned to the fundamental frequency component of the periodic wave. Harmonic number 0 represents the constant or DC component of the waveform. The DC component is the net difference between the positive and negative halves of one complete waveform cycle.

Figure 4.5 shows a periodic waveform with net DC content. The DC component of a waveform has undesirable effects, particularly on transformers, due to the phenomenon of core saturation. Saturation of the core is caused by operating the core at magnetic field levels above the knee of the magnetization curve. Transformers are designed to operate below the knee portion of the curve.

When DC voltages or currents are applied to the transformer winding, large DC magnetic fields are set up in the transformer core. The sum of the AC and the DC magnetic fields can shift the transformer operation into regions past the knee of the saturation curve. Operation in the saturation region places large excitation power requirements on the power system. The transformer losses are substantially increased, causing excessive temperature rise. Core vibration becomes more pronounced as a result of operation in the saturation region.

We usually look at harmonics as integers, but some applications produce harmonic voltages and currents that are not integers. Electric arc furnaces are examples of loads that generate non-integer harmonics. Arc welders can also generate non-integer harmonics. In both cases, once the arc stabilizes, the non-integer harmonics mostly disappear, leaving only the integer harmonics.

The majority of nonlinear loads produce harmonics that are odd multiples of the fundamental frequency. Certain conditions need to exist for production of even harmonics. Uneven current draw between the positive and negative halves of one cycle of operation can generate even harmonics. The uneven operation may be due to the nature of the application or could indicate problems with the load circuitry. Transformer magnetizing currents contain appreciable levels of even harmonic components and so do arc furnaces during startup. Sub-harmonics have frequencies below the fundamental frequency and are rare in power systems.

When sub-harmonics are present, the underlying cause is resonance between the harmonic currents or voltages with the power system capacitance and inductance. Sub-harmonics may be generated when a system is highly inductive (such as an arc furnace during startup) or if the power system also contains large capacitor banks for power factor correction or filtering. Such conditions produce slow oscillations that are relatively un-damped, resulting in voltage sags and light flicker.

Causes of Voltage and Current Harmonics:

A pure sinusoidal waveform with zero harmonic distortion is a hypothetical quantity and not a practical one. The voltage waveform, even at the point of generation, contains a small amount of distortion due to non-uniformity in the excitation magnetic field and discrete spatial distribution of coils around the generator stator slots. The distortion at the point of generation is usually very low, typically less than 1.0%.

The generated voltage is transmitted many hundreds of miles, transformed to several levels, and ultimately distributed to the power user. The user equipment generates currents that are rich in harmonic frequency components, especially in large commercial or industrial installations. As harmonic currents travel to the power source, the current distortion results in additional voltage distortion due to impedance voltages associated with the various power distribution equipment, such as transmission and distribution lines, transformers, cables, buses, and so on.

Figure 4.9 illustrates how current distortion is transformed into voltage distortion. Not all voltage distortion, however, is due to the flow of distorted current through the power system impedance. For instance, static uninterruptible power source (UPS) systems can generate appreciable voltage distortion due to the nature of their operation. Normal AC voltage is converted to DC and then reconverted to AC in the inverter section of the UPS. Unless waveform shaping circuitry is provided, the voltage waveforms generated in UPS units tend to be distorted.

As nonlinear loads are propagated into the power system, voltage distortions are introduced which become greater moving from the source to the load because of the circuit impedances. Current distortions for the most part are caused by loads. Even loads that are linear will generate nonlinear currents if the supply voltage waveform is significantly distorted.

When several power users share a common power line, the voltage distortion produced by harmonic current injection of one user can affect the other users. This is why standards are being issued that will limit the amount of harmonic currents that individual power users can feed into the source.

The major causes of current distortion are nonlinear loads due to adjustable speed drives, fluorescent lighting, rectifier banks, computer and data-processing loads, arc furnaces, and so on. One can easily visualize an environment where a wide spectrum of harmonic frequencies are generated and transmitted to other loads or other power users, thereby producing undesirable results throughout the system.