Boundary Layer Fluid Flow: Notes, Layer Thickness, Equations and Solved Problems and examples.
Introduction to Boundary Layer:
In an ideal fluid shear stresses are totally absent. So when an ideal fluid should flow over a boundary there are no resistances between the boundary and the fluid and the fluid simply slips smoothly over the boundary surface. But, when a real fluid flows over a boundary due to the viscosity of the fluid, it sticks to the boundary and therefore has no velocity at the boundary.
The velocity of the fluid increases from zero at the boundary surface to a terminal value within a small thickness. This thin layer of the fluid adjacent to the boundary surface within which the velocity of the fluid increases from zero to a terminal value is called the boundary layer.
Consider a fluid moving with a velocity U. As the fluid moves past a solid boundary, the velocity of the fluid is disturbed for a certain distance from the surface of the boundary. For example consider the section XX. At this section the velocity is disturbed for a distance δ from the boundary. Within this distance the velocity of the fluid will vary from zero at the surface of the solid boundary to the velocity U. This layer of fluid within which the velocity variation takes place is known as the boundary layer.
ADVERTISEMENTS:
It is in the boundary layer the entire viscous or frictional resistance between the moving fluid and the solid boundary surface, occurs. The type of flow within the boundary layer may be stream line flow or turbulent flow depending on the particular problem or the distance from the leading edge of the solid boundary.
Under certain conditions, the boundary layer may leave the surface and coil up into a vortex or whirlpool. This phenomenon is called separation or break away of the boundary layer. The thickness δ of the boundary layer increases with the distance from the leading edge. It is proportional to the square root of the distance x from the leading edge and is also dependent on the Reynold’s number ρUx/μ.
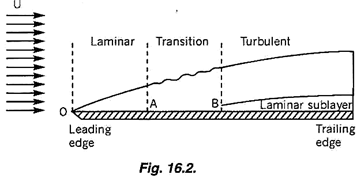
Fig. 16.2 shows a fluid flowing past a horizontal plate and the boundary layer of the flowing fluid. For a certain distance from the leading edge O to A the laminar boundary layer prevails. Beyond the point A the laminar boundary layer becomes unstable and the flow properties are between those of laminar and turbulent flows. This condition prevails for a certain distance AB (which is nearly equal to OA). This region is called the transition zone.
ADVERTISEMENTS:
Beyond the point B the flow in the boundary layer is turbulent. This part of the boundary layer is considerably thicker. If the plate is sufficiently smooth it is seen that within the thickness of the turbulent boundary layer there exits an extremely thin layer adjacent to the plate within which a laminar flow occurs and this thin layer is called laminar sub-layer.
For a plate of short length, the flow within the boundary layer may be laminar throughout its length. In the case of a long plate the flow may pass through all the three stages, namely laminar, transition and turbulent after which a break away may take place as shown in Fig. 16.3.
The type of flow in the boundary layer is dependent on the value of the Reynold’s number ρUx/μ.
ADVERTISEMENTS:
where,
ρ = Density of the fluid
U = Approach velocity of the fluid
ADVERTISEMENTS:
μ = Viscosity of the fluid
x = Distance from the leading edge.
When the Reynold’s number is less than 3 x 105 the flow in the boundary layer is laminar. When the Reynold’s number is greater than 5 x 105 the flow in the boundary layer is turbulent. It is very difficult to predict the exact value of the Reynold’s number at which the flow changes from laminar to turbulent flow. For purposes of analysis however we may assume the critical value of the Reynold’s number to be equal to 5 x 105.
Thickness of the Boundary Layer:
The thickness of the boundary layer is the distance from the supporting boundary surface within which the velocity variation occurs. If the approach velocity is U and the thickness of the boundary layer at a section is δ, then it means, within this distance δ from the supporting surface the velocity varies from zero to U.
ADVERTISEMENTS:
In the actual cases, it is very difficult to determine this distance. In fact the velocity varies reaching the value U asymptotically. Hence for purpose of analysis the distance from the supporting surface at which the velocity of the fluid is 0.99 U may be taken as the thickness of the boundary layer. See Fig. 16.4.
Displacement Thickness δ*:
Consider a fluid moving with a velocity U approaching a flat plate at rest as shown in Fig.16.5.
At a section distance x from the leading edge, let δ be the thickness of the boundary layer. At this section the velocity varies from zero at the plate to U at a distance δ from the plate.
Consider unit width of the plate. Consider an elemental strip (1 x dy) distance y from the plate. Let u be the velocity at this level.
Mass flowing per second through the elemental strip = ρudy
If the plate had not been present the mass flowing per second through the above elemental strip would have been ρUdy.
∴ Reduction in mass flowing per second through the elemental strip
= ρ(U – u) dy
∴ Total reduction in mass flowing per second due to the plate –
Suppose the plate is displaced normal to itself by δ* and the velocity is uniform at the value U, then the mass of fluid passing through the strip of thickness δ* will be ρUδ *. The depth δ* is called displacement thickness.
Momentum Thickness θ*:
Again consider the flow through an elemental strip of area (1.dy) distance y from the boundary.
Mass flowing per second through the elemental strip = ρudy
Let us consider the above quantity of the fluid.
Momentum of this quantity = (ρudy) u = ρu2dy
Momentum of this quantity in the absence of the boundary layer = (ρudy) U
Loss of momentum per second-
The momentum thickness θ* may be visualized as the depth of flow with uniform velocity U, so as to have a momentum per second equal to the loss of momentum per second due to boundary layer. For a depth of flow θ* with a velocity V momentum per second per unit width
= (ρθ*U) = ρU2θ*
The depth θ* is called momentum thickness.
Energy Thickness δ**:
Again consider the flow through an elemental strip (1.dy) distant y from the boundary. Mass flowing per second through the elemental strip (ρudy)
Suppose δ** is the depth of flow with uniform velocity U so as to have a kinetic energy equal to the loss of kinetic energy due to the boundary layer.
Drag Force due to Boundary Layer:
Consider a fluid moving past a plate of width b as shown in Fig. 16.6. Let U be the approach velocity of the fluid. At a distance x from the leading edge let δ be the thickness of the boundary layer. Now let us consider an elemental strip of area bdy normal to the direction of flow and at a distance y from the plate. Let u be the velocity at this distance from the plate.
Laminar Boundary Layer Analysis for Various Laws of Velocity Distribution:
The velocity distribution in the boundary layer is taken according to various laws.
Pohlhausen suggested the following general law for the velocity distribution:
Turbulent Boundary Layer:
When turbulent flow takes place in the boundary layer, the shear stress is the result of momentum exchange between the various layers of the fluid. In this case the velocity of the fluid at a distance y from the boundary is taken to follow the law,