Classification or Types of Notches and Weirs | Fluid Mechanics

Classification or Types of Notches and Weirs in Fluid Mechanics.

A notch means an opening provided in the side of a tank, such that the opening extends even above the free surface of the liquid in the tank. It is in a way, a large orifice having no upper edge. A notch is generally meant to measure the flow of water from a tank. A weir is also a notch but it is made on a large scale. The weir is a notch cut in a dam to discharge the surplus quantity of water.

Water flows over a notch or weir while water passes through an orifice. While the stream of water discharged by an orifice is called a jet, the sheet of water discharged by a notch or weir is called a nappe or vein. The upper surface of the notch or weir over which the water flows is called the Crest or Sill.

A notch or a weir is a convenient device for the measurement of discharge in an open channel. A notch or a weir is an obstruction provided in a channel that causes the water to rise behind it so that the water is made to flow through it or over it. The rate of flow can be determined by measuring the height of the upstream water level.

Basically there is no difference between a notch and a weir, except that a notch is of small size while a weir is of large size. A notch is usually made of metal plate whereas a weir is made of masonry or concrete.

The bottom edge over which the water flows is called the sill or the crest of water the notch. The common shapes of weirs are, rectangular, triangular, trapezoidal, composite, parabolic and proportional. The sheet of water which springs free from the crest is called the nappe.

If the sheet of water springs free as it leaves the crest, the weir is called a sharp crestel weir. In the case of a broad crested weir, there is a support for the falling nappe over the crest in the direction of flow. As the water approaches the crest there is a fall in the water surface forming a convex curve called the draw down. The draw down at the weir crest is about 0.15H where H is the head of water surface above the crest.  

Weirs may be classified in many ways. They can be classified as rectangular, triangular and trapezoidal weirs based on the geometry of flow section. They can be classified into sharp crested and broad-crested weirs based on the sharpness of the crest. They can be classified into straight and curved weirs based on their shape in plan. They can be classified into waste weirs and gauging weirs based on the purpose for which they are provided.

A waste weir is provided for discharging the surplus quantity of discharge from a reservoir. A gauging weir is meant for gauging the rate of flow of water. Weirs may also be classified into suppressed weirs and weirs with lateral contraction.

Classification of Notches:

1. The Rectangular Notch:

2. The Triangular Notch or V-Notch:

3. The Trapezoidal Notch:

Consider a trapezoidal notch whose crest length is l and the sides are at θ with the vertical. Let H be the head of water over the crest.

In this case the notch may be taken to consist of a rectangular notch of length l and a triangular notch subtending an angle 2θ.

Advantages of a Triangular Notch over Rectangular Notch:

A triangular notch has certain advantages over the rectangular notch when used as a gauging device in a hydraulic laboratory.

The advantages are:

(i) The coefficient of discharge for a triangular notch is practically independent of the head. This is because, for all heads the ratio of the head to the wetted length or crest is constant. But in a rectangular notch the ratio of the head to the wetted length crest is not constant. Hence for a rectangular notch the coefficient of discharge is not actually a constant but is a function of the head over the notch.

(ii) When the discharge rate is small a triangular notch provides a greater head than the rectangular notch. Hence head measurement can be done more accurately over the triangular notch than over the rectangular notch.

(iii) When the discharge rate is small, there are chances of a clinging nappe to be formed when a rectangular notch is used. But for the same discharge over the triangular notch the head will be greater and the clinging nappe will be avoided.

(iv) When a triangular notch is provided, there will be no need for any special arrangement for ventilating the nappe.

Classification of Weirs:

1. Proportional Weir:

This is a weir whose shape is so designed that the discharge over the weir is proportional to the head of water over the crest. The crest of the weir is horizontal.

Consider the weir shown in Fig. 9.13, whose equation with the middle point of the crest as origin is x² = K/y where K is a constant. Let H be the head of water over the weir. Consider a horizontal strip of the flow section of width 2x at a height y above the crest. Let dy be the thickness of the strip. Discharge through the elemental horizontal strip.

Thomson’s Principle of Geometric Similarity:

Weirs are said to be geometrically similar when the ratio of their corresponding linear dimensions remains the same. Consider two geometrically similar weirs. Let their lengths be L and I. Let the heads on the weirs be H and h.

Let discharge Q and q over them are given by –

Velocity of Approach:

Consider a weir provided across a river. The water which is approaching the weir possesses a certain velocity known as the velocity of approach. The discharge over the weir is increased due to the velocity of approach.

Let v_a be the velocity of approach. This condition is equivalent to a condition in which the free water surface is static at a higher level, at a height h_a = v_a²/2g. The head h_a is called the head due to the velocity of approach. If the head of the actual flowing water level over the crest is H, the weir opening may be taken as equivalent to a large orifice in which the heads of still water above the top and bottom edges are respectively, h_a and H + h_a.

Accordingly, the discharge is given by,

The quantity H + h_a is called still water head.

The velocity of approach can be determined by dividing the discharge by the area of flow of water in the stream on the upstream side of the weir. We may first calculate the discharge ignoring the velocity of approach. This approximate value of the discharge is divided by the area of the approach channel and an approximate value of the velocity of approach is determined.

The corresponding head due to the velocity of approach is calculated. Now a more accurate value of the discharge is calculated from the above equation. This process may be repeated to get more accurate value of the discharge.

Francis Formula—End Contractions:

We know for a rectangular notch of length I the discharge over the notch is given by,

When the length of the weir is less than the width of the stream, we find there will be a lateral contraction at each end such a weir is called a contracted weir. According to Francis each lateral contraction (also called end contraction) is equal to 0.1 H.

If the actual length of the weir is l, then the effective length of the weir will be (I – 0.2 H). In some cases there may be intermediate obstacles like piers over the weir. In such a case if l is the length of the weir after making deductions for the widths of the obstacles and if there are n lateral contractions the effective length of the weir will be (l – 0.1 nH).

Fig. 9.17 Shows the standard proportions for a contracted weir.

Hence the discharge over the weir will be –

The above formula is called Francis formula.

If the velocity of approach is also considered, then

q = 1.84 [l – 0.1 n (H + h_a)] [(H + h_a)^3/2 – h_a ^3/2]

If the length of the weir is exactly equal to the width of the approaching stream, there will not be any end contractions. Such a weir is called a suppressed weir, and for such a weir Francis formula simplifies to q = 1.84 I H^3/2.

Bazin’s Formula:

We know the discharge over a rectangular weir is given by –

Rehbock Formula:

The discharge over the weir as per this formula is given by –

2. The Cippoletti Weir:

We know for a rectangular weir with the two end contractions, the discharge is given by –

3. Submerged Weir:

Fig. 9.19 shows a submerged weir. In this case the water level on the downstream side also is above the crest of the weir. Let H₁ and H₂ be the heights of the upstream and downstream water levels above the crest weir. The total discharge Q consists of components Q₁ and Q₂.

4. Anicut or Raised Weir or Barrage:

An anicut is a masonry dam provided across a river for the purpose of raising the water level on the upstream side to a sufficient extent in the dry season, so that the water can be carried by gravitation to places where it otherwise could not reach.

Example:

Anicut at Okhla on Jamuna River (Delhi); anicut at Rasul on Jhelum River in Punjab; anicut at Ferozepur on Sutlej river. Water required is taken off by a channel on one or both sides just above the anicut, the opening from the river being provided with a masonry head sluice to regulate the admission of water.

In case the full surplus level in the channel is to be maintained even when the discharge in the river is low, the anicut level should be slightly above the proposed full supply level in the channel.

All the surplus quantity of water will pass over the anicut. In ordinary seasons the surplus quantity of water may discharge with a free over fall; but during floods the tail water level may be above that of the anicut, and the water is heaped up on the upstream side until the head created is adequate to pass the river discharge through the restricted section.

In certain cases flash boards are provided over the crest of the weir to regulate the full supply level in the river and the channel during the dry season. These flash boards are removed during floods, and the depth of flood water over the crest maintains the full supply level in the offtake channels above the weir which are also properly controlled by the head regulators.

Sometimes masonry structures are built on the top of the raised weir in which openings fitted with sluice gates are provided. These openings are arched over and support a road bridge or foot bridge. In some cases these sluice gates are operated by a crane. Such an arrangement is helpful to regulate the full supply level or the flood level in the river as well as in the channels which take off from the river.

Time of Emptying a Reservoir by a Rectangular Weir:

Let a reservoir of plan area A be provided with a rectangular weir of length I. Let it be required to find the time taken for the head of water over the weir to fall from a value H₁ to a value H₂.

Let at any instant the head of water over the weir be h. Let the fall in water level be dh in a small interval of time dt

Time of Emptying a Reservoir by a Triangular Notch:

Let a reservoir of plan area A be provided with a triangular notch of angle θ. Let it be required to find the time taken for the head of water over the notch to fall from a value H₁ to a value H₂. Let at any instant the head of water over the notch be h. Let the fall in water level be dh in a small interval of time dt.

5. Broad Crested Weir:

This is a weir having a very broad sill so that the flow of water over the sill may be compared to the flow of water in a channel. Consider the broad crested weir shown in Fig. 9.25.

Let H be the head of water over the weir. Let I be the length of the weir. As the water flows over the weir, it reaches a uniform depth of flow h, over the crest. Let v be the uniform velocity of flow over the weir.

Applying Bernoulli’s equation to the still water surface on the upstream side and the running liquid surface at the outlet.

6. Ogee Weir:

We know, in the case of a sharp crested weir the nappe as it leaves the crest springs or rises slightly at the lower surface. In this way it reaches a maximum rise of 0.115 H’ above the crest and then falls. (H’ is the head over sharp crest). Suppose the space below the bottom surface of the nappe be filled with masonry or concrete.

The consequent weir formed is shown in Fig. 9.26. Such a weir is called an ogee weir. Thus in an ogee weir, the solid boundary of the weir exactly coincides with the bottom surface of the nappe of the sharp crested weir under the designed head.

If H’ is the head above the sharp crest then by Francis formula the discharge is given by, q = 1.84 lH’^3/2. Alternatively if the head H above the spillway be considered then the discharge is given by, q = 2.20 lH^3/2.

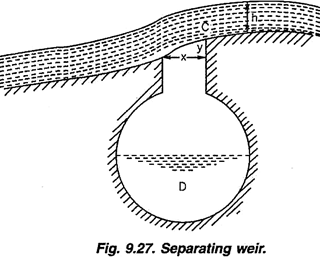
7. Separating Weir:

A separating weir is an arrangement provided in the case of town water supply, where it may become necessary to divert the discoloured flood water from the supply channel. When the discharge is moderate, the water drops over the lip C into a culvert D which communicates with the supply channel.

But during floods, the velocity of flow will be greater due to greater depth and this causes the water to leap across the opening into the waste channel.

The average velocity of the water sheet of depth h when it leaves the drain may be taken as ⅔√2gh. Let the time taken by the sheet of water to jump across the opening be t seconds. Let x and y be horizontal and vertical displacement in this interval.