List of top four problems on PERT.
Example 1:
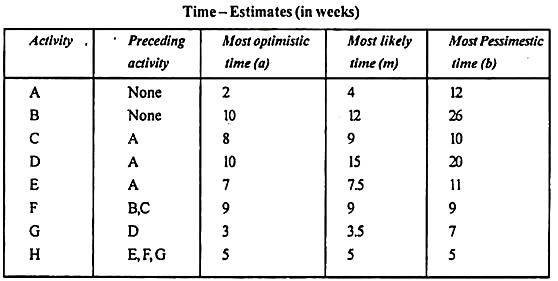
A small project consisting of eight activities has the following characteristics:
(i) Draw the PERT network for the project.
ADVERTISEMENTS:
(ii) Prepare the activity schedule for the project.
(iii) Determine the critical path.
(iv) If a 30- week deadline is imposed, what is the probability that the project will be finished within the time limit?
ADVERTISEMENTS:
If the project manager wants to 99% sure that the project is completed on the schedule date, how many weeks before that date should he start the project work?
Solution:
The network diagram for the given data is shown in fig. below. The earliest time and variance of each activity is computed by using the formula.
(ii) Calculation activity duration and scheduling times.
(iii) The critical path of the project is 1-2-4-5 -6, critical activities being A, D, G and H.
The expected project length is the sum of duration of each critical activity. Expected project length = 5 + 15 + 4 + 5 = 29 weeks.
Variance project length is obtained by summing variance of each critical activity.
(Iv) The required probability can be determined by finding the area under the normal curve to the left of X = 30
Now, the probability of completing the project within the 30 week deadline is
(v) If the project start T weeks before the due date, the X will represent the ordinate under normal curve to the left of which 99% of area lies.
ADVERTISEMENTS:
The area between n and X- being 99-50 or 49% and Z – value corresponding to this is 2033 (From table)
Example 2:
A small project consisting of ten activities has the following characteristics:
Determine the critical path
Solution:
Network for the given project is drawn below:
Value of expected time for each activity is shown in following Table:
Time [Earliest & latest] are calculated as follows:
As we can see there are two critical paths along which E-values and L-values are similar, but the longest network of critical activities is known as critical path.
Critical path is 1-2-3-6-7-8
Expected length of critical path is = 6 + 3 + 4 + 2 + 2 = 17 weeks
Example 3:
Product manager has planned a list of activities culminating in the inaugurate launch of the new products.
These are given in the table below:
What is the probability that product manager will be able to complete the language launch within 80 days-time?
Solution:
Network diagram for given problem is shown in following fig:
Expected time value for each activity of given network is listed in table below along with three variance.
Value of earliest & latest time is calculated on the basis of expected time te as follows:
Value of earliest & latest time is calculated on the basis of expected time te as follows:
Hence critical path along with E-value and L- value are same i.e., 1- 2-4-5-6-7- 8-9 Expected project duration is 172.83 days
Variance of project length = Sum of variance of each critical activity = 6.25 + 0.44 + 32.11 +100+1.36+.44+0= 140.6
For Z = -2.77 Probability of completing the project with 80 days-time i.e., 0.3%.
Example 4:
A Project is composed of seven activities whose time estimates are listed in the following table. Activities are simplified by this beginning (1) ones ending (j) Node member.
Calculate expected project length.
Solution:
Calculation of expected time for each activity is shown in following table:
E- Values and L- values are calculated on the basis of expected time are as follows:
Network diagram for given project along with E-values and L-values is shown by following Fig:
Critical path for the above network 1-3-5-6 shown by double lines; along with E- values and L-values are same.
Expect project length will be = 4 + 6+ 7 = 17 weeks.