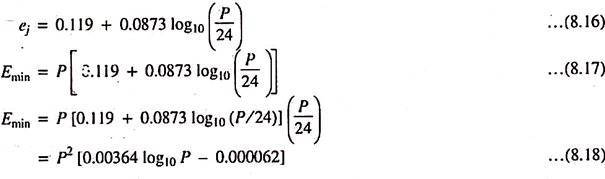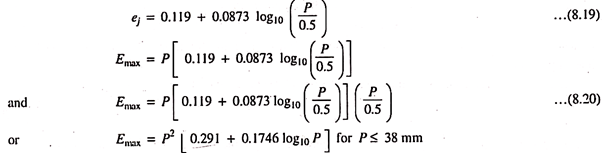The rainfall erosivity is related to the kinetic energy of rainfall. The following two methods are widely used for computing the erosivity of rainfall: 1. EI30 Index Method 2. KE > 25 Index Method.
1. El30 Index Method:
This method was introduced by Wischemeir (1965). It is based on the fact that, the product of kinetic energy of the storm and the 30-minute maximum rainfall intensity provides a best estimate of soil loss. The highest average rainfall intensity in any 30-minute period during the storm may be computed from the recording type rain gauge charts or mass curve, (Fig. 8.4) just by knowing the amount of rain, which has fallen in period of 30-minutes and then converting the same in the form of intensity (mm/h), which is done by doubling the same amount. After determining the rainfall intensity for 30-minute duration, the kinetic energy of storm is computed as KE = 916 + 331 log10I.; in which, I stands for rainfall intensity, inch/h.
The rainfall erosivity is determined as the product of KE and maximum 30-minutes rainfall intensity. This method of estimating, the rainfall erosivity is referred as EI30 index method. The erosivity is computed for individual daily storms and then added altogether to get the weekly, monthly or annual erosivity values.
2. K.E. > 25 Index Method:
ADVERTISEMENTS:
The El30 index method has limitation that it was developed for American conditions and is not found suitable for tropical and sub-tropical zones for estimating the erosivity. The K.E. > 25 index method is an alternate method, was introduced for computing the rainfall erosivity of tropical storms, by Hudson.
This method is based on the concept, that the erosion takes place only at threshold value of rainfall intensity. From experiment, it was obtained that the rainfall intensities less than 25 mm/h are not able to detach the soil particles. Thus, this method takes care only those rainfall intensities, which are greater than 25 mm/h. That is why its name became as K.E. > 25 index method. The estimation procedure is same to the El30 index method.
Calculation Procedure:
The calculation procedure of rainfall erosivity is same for both the methods. However, K.E. > 25 method is more advantageous, because it sorts out those rain events which intensity is less than 25 mm/h, hence requires less rainfall data. However, for both the methods it is necessary to have the informations on rainfall amount and its intensity.
ADVERTISEMENTS:
The procedure involves the multiplication of rainfall amounts in each class of intensity to the computed kinetic energy values; and then all of them are added together to get total KE of storm. The kinetic energy obtained so, is again multiplied by the maximum 30-minute rainfall intensity to determine the rainfall erosivity value.
Rainfall Erosion Index and Rainfall Amount:
Earlier, the computation of El30 was described with the use of maximum rainfall intensity (l30), which is for 30-minutes duration. Normally, the availability of rainfall intensity data is very scare, as result the computation of l30 is not possible.
Therefore, in absence of intensity data, how El30 could be determined is very important. In this direction, several developments have been made and also been derived the solutions; few of them are cited as under –
ADVERTISEMENTS:
Richardson et.al. (1983) derived following relationship between rainfall depth (P) and the erosion index (EI):
EI = a Pb + e. … (8.15)
Where,
a Pb = a deterministic component
ADVERTISEMENTS:
e = a random component of the equation. It is the difference between the observed and predicted EI based on the deterministic component (i.e. a Pb).
Thus, if a and b are known and the statistical distribution of e is identified, then the estimate of El can be obtained from the rainfall amount (P).
Minimum EI for Daily Rainfall Amount:
It is the El, which is resulted from the rainfall event of amount P that would occur during a rainfall of uniform intensity lasting for the full 24-h period. For this condition, ij = I30 = (P/24). Can be written as –
Maximum EI for Daily Rainfall Amount:
It is resulted from the rainfall events occurring either in 30 minutes duration or less period. In this condition, the rainfall intensity is less than 76 mm/h, P ≤ 38 mm and ij = I30 = P/0.5
We have –
Ram Babu et. al. (1969) derived the relationship between EI30 and daily and monthly rainfall amounts for Dehradun region (India), given as under:
(i) For Daily rainfall amounts –
Y1 = 3.1 + 0.533 X1 … (8.23)
(ii) For monthly rainfall amounts –
Y2 = 1.9 + 0.640 X2 … (8.24)
in which, Y1 and Y2 are the values of El30 for daily and monthly rainfall amounts, respectively and X1 and X2 are the daily and monthly values of rainfall (mm), respectively.
Bollinne et.al (1980) presented the relationship between El30 and mean annual precipitation, given as –
El30 = 159.56 + 0.27 P … (8.25)
(r = 0.99)
in which, P stands for mean annual precipitation (mm).
Ateshian (1974) also developed empirical equations for estimating the average R-factor, given as below:
R = 27.00 P2 . 2 … (8.26)
and R = 16.55 P2 . 2 … (8.27)
in which, P is the 6-h rainfall (inch) with a return period of 2-year. Equation 8.26 is fit for the main lands of United States except for the coastal areas of the Sierra, Nevada and Cascade Mountain. The equation 8.27 holds good for the island of Hawaii and Alaska regions.
Charreau (1969), CTFT (1974), Galabert and Millogo (1973) and Roose (1977 a, b) derived a linear relationship between kinetic energy and the rainfall magnitude for semi-arid regions of the West Africa.
The relationship is given as under:
R = 0.0158 H I30 – 1.2 … (8.28)
in which, R is the erosivity factor and H is used to denote the magnitude of rainfall.
Roose (1977 a, b) also developed a linear relationship between R and the rainfall amount for the rainy period from June to September. The equation is given by –
R = 0.577 H – 5.766 … (8.29)
This equation is valid for the humid coastal regions of Ivory coast. He also derived an empirical relationship between average annual erosivity index Rav and corresponding average annual rainfall Hav, given as under –
Rav/Hav = 0.55 ± 0.05 … (8.30)
Similarly, for east Java, Utomo and Mahmud (1984) have also derived the relationship between R and weekly, monthly and annual rainfall magnitudes. These are written as –