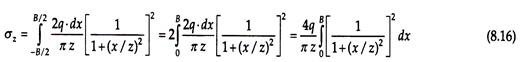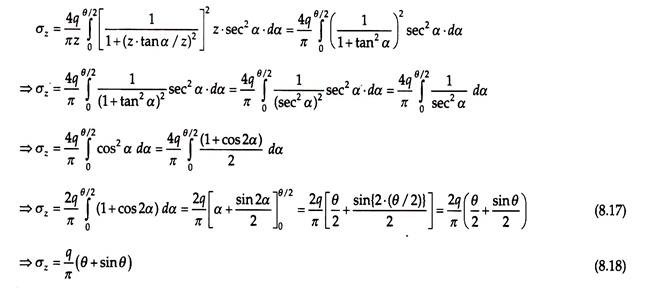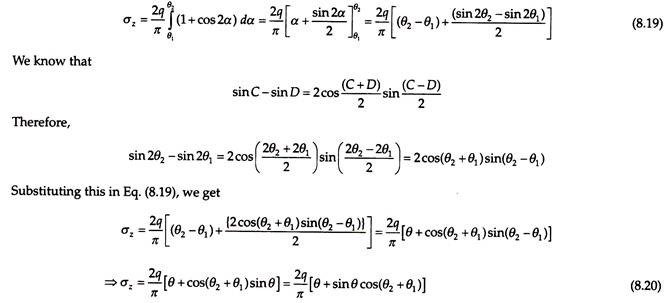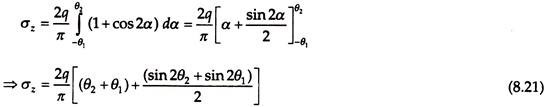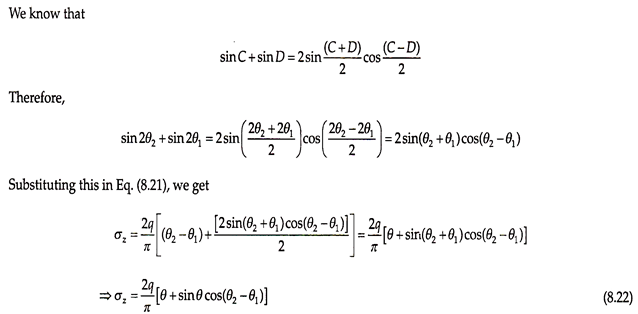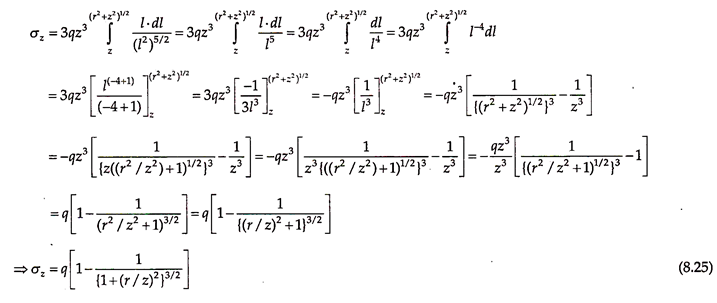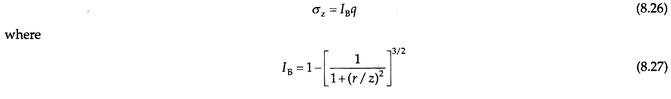Strip footing is used to support walls or retaining walls where length is considerably more than the width. The load is considered per unit area per unit length, say 1 m. Thus, the units for load are kN/m2 in SI system.
Vertical Stress below Center of Strip Footing:
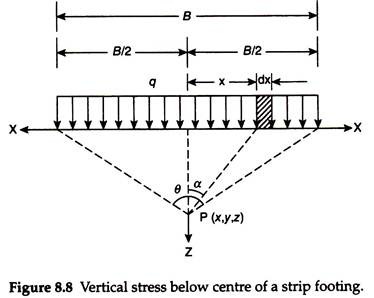
Consider a strip footing of width B subjected to a uniform pressure q, including self-weight, as shown in Fig. 8.8. The strip load acts over the length of the strip footing in the perpendicular direction along y-axis. It is required to determine the vertical stress at a point P which is at depth z below the center of the footing. Let θ is the angle subtended by the edges of the strip footing at point P.
Consider an elemental load over a small width dx at any distance x from the center of the footing, at an angle α with z-axis. The total elemental load over this small width extending across the length of the footing is qdx. This may be considered as line load. The vertical stress at point P, due to this elemental line load, can be obtained using Eq. (8.13) as –
The total vertical stress at point P due to the entire load is given by –
In Fig.8.8,
tan α = x/z Þ x = z . tan α
Also dx = z . sec2 α . dα. Substituting the values of x and dx in Eq. (8.16), we get –
where q is the load intensity (kN/m2) from the strip footing at the ground surface and θ is the angle subtended by point P with the edges of the footing.
Vertical Stress below Strip Footing at a Point Outside the Edges:
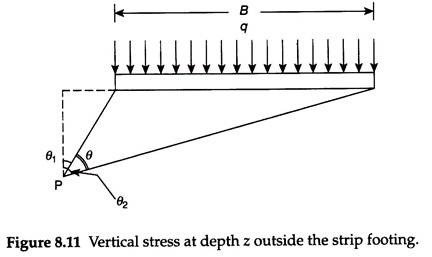
Figure 8.11 shows a strip footing subjected to a uniform load of intensity q per unit area. It is required to determine the vertical stress at any point P, which is not below the center of the footing.
Let θ1, θ2 be the angles subtended by the edges of the footing with z-axis at point P and θ be the total angle subtended by the edges of the footing at point P.
ADVERTISEMENTS:
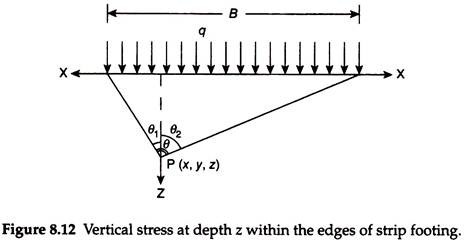
The vertical stress at point P can be obtained by integrating Eq. (8.17) between the limits θ1 and θ2:
In Eq. (8.20), both the angles θ1 and θ2 are clockwise and positive.
ADVERTISEMENTS:
It may be seen that if θ1 = – θ2, point P will be below the center of the footing and the equation for vertical stress becomes –
σz = q/π(θ + sinθ cosθ) = q/π (θ + sinθ)
which is the same as Eq. (8.18).
Vertical Stress below Strip Footing within the Edges:
Figure 8.12 shows a strip footing exerting a pressure q on the soil. It is required to determine the vertical stress at point P, which is within and between the edges of the footing at any depth z, as shown in Fig. 8.12.
The vertical stress at point P is obtained by integrating Eq. (8.17) between the limits –θ1 and θ 2 as follows –
It may be seen that if θ1 = θ 2, point P will be below the center of the footing and the equation for vertical stress becomes –
σz = q/π (θ + sinθ cosθ) = q/π (θ + sinθ)
which is the same as in Eq. (8.18).
Vertical Stress Distribution on Vertical Plane below Strip Footing:
1. Case I – Below the Center of a Strip Footing:
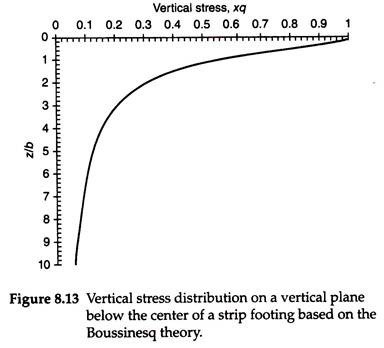
The vertical stress below the center of a strip footing can be determined at depths z/b = 0.05, 0.1, 0.2, etc. up to z/b = 10 by substituting the corresponding angle in Eq. (8.18). Figure 8.13 shows the vertical stress distribution thus obtained on a vertical plane below the center of a footing as a function of z/b.
It may be observed from Fig. 8.13 that the vertical stress, which is equal to q immediately below the footing, decreases sharply to about 0.55q at z/b = 1 and to 0.3q at z/b = 2. Thereafter, there is a gradual decrease in the vertical stress with the increase in z/b. It may also be observed that the intensity of the vertical stress is 0.2q at z/b = 3 and 0.1 q at z/b = 5.6.
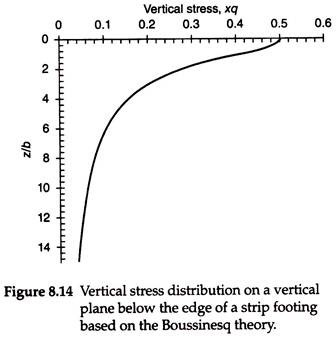
2. Case II – Below the Edge of a Strip Footing:
Figure 8.14 shows the vertical stress due to a strip load below the edge of a footing with z/b. It may be observed that the vertical stress decreases considerably from 0.5q at z/b = 0.05 to about 0.41q at z/b = 1and 0.1q at z/b = 6.
Vertical Stress Distribution on a Horizontal Plane:
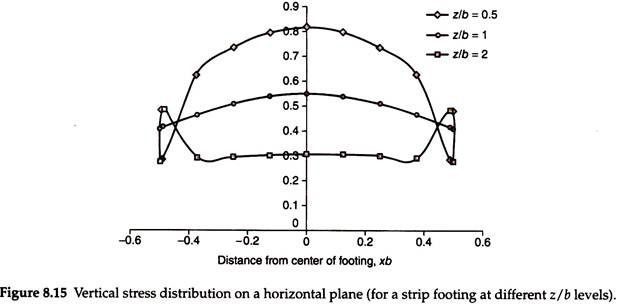
Equation (8.22) can be used to obtain vertical stress at different points on a horizontal plane at a given depth, say z/b = 1. Figure 8.15 shows the vertical stress distribution below a strip footing on a horizontal plane at three depths z/b – 0.5, 1, and 2. Here, the vertical stress is represented on the y-axis as a multiple of q and the x-axis represents distance from the center of the footing as a multiple of b, the width of the footing.
It may be seen that the vertical stress changes significantly over the width of the footing when z/b = 0.5. It changes only marginally over the width of the footing at z/b = 1 and 2. The distribution becomes erratic toward edges at z/b = 2 as shown in Fig. 8.15.
Vertical Stress below the Center of a Uniformly Loaded Circular Area:
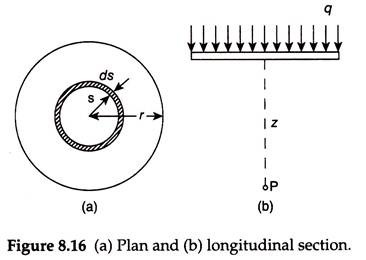
Consider a circular footing of radius r at the ground surface exerting a uniform pressure q. Consider an elemental part of this load consisting of annular strip of very small width ds at any radial distances from the center, as shown in Fig. 8.16.
The total load acting on this elemental annular strip is q × 2 πs × ds. This load can be considered as a concentrated load acting at a constant radial distance of s from the center. The elemental vertical stress due to this load at point P, which is at any depth z below the center of the footing, can be obtained using Eq. (8.7) as –
Differentiating on both sides, we get –
2.s.ds = 2.l.dl (since z is constant and its differential is zero)
or s.ds = l.dl
From Eq. (8.24), when s = 0, l = z; and when s = r,
l = (r2 + z2)1/2
Substituting these values in Eq. (8.23), the vertical stress at point P is given by –
Thus, the vertical stress at depth z below the center of the circular footing is given by –
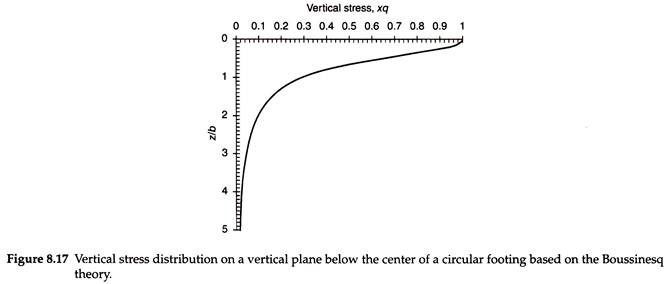
Here q is the load per unit area, r is the radius of the circular footing, and z is the depth below the center of the footing. Figure 8.17 shows the stress distribution on a vertical plane below the center of a circular footing on the x-axis as a function of z/b on the y-axis, where b = 2r = width of the footing.
It may be observed from Fig. 8.17 that the vertical stress decreases rapidly from q at the bottom of the footing to 0.5q at z/b = 0.7,0. 3q at z/b = 1.0, and 0.2q at z/b = 1.3. The vertical stress is equal to 0.1q at z/b = 1.8.
Vertical Stress below the Corner of Uniformly Loaded Rectangular Area:
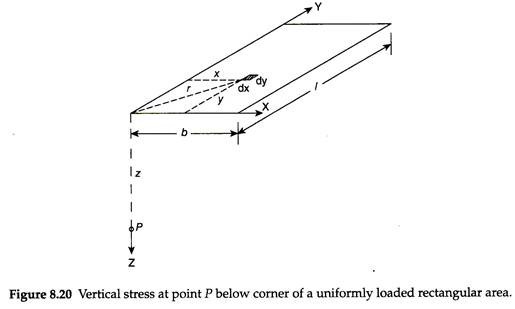
Figure 8.20 shows a uniformly loaded rectangular area of dimensions I and b, subjected to a uniform pressure q. It is required to determine the vertical stress at point P having coordinates (x, y, z) below the corner of the rectangular area at any depth z below the load.
Consider an elemental area of very small dimensions dx and dy of the loaded area at any horizontal radial distance, r at distances x and y along the x and y axes from the corner. The total load acting on the elemental area is q × dx × dy. This load can be considered as a concentrated load. The vertical stress due to this elemental load at point P can be obtained using Eq. (8.7) as –
The vertical stress at point P due to the entire load is given by –
The solution of the above double integral is obtained by Newmark, which is very complicated. The final expression for vertical stress at point P is given by –
σ = IBq …(8.29)
Now, q is the intensity of pressure on the rectangular area and IB is the Boussinesq influence factor.
Now –
x = m2 + nz + 1; y = m2n2; m = l/z; n = b/z …(8.30b)
where l is the length of footing, b is the width of footing, and z is the depth of point P vertically below the corner of the footing. In evaluating IB using Eq. (8.30), the second term obtained in degrees should be converted to radians. Also at some higher values of m and n, the second term becomes negative as the tangent of an angle is negative in the second quadrant. The angle should be converted to a positive value by adding 180° (π radians) to the negative value for obtaining the correct value of IB.
For example, for m = 1.2 and n = 2.4, the second term within parentheses of Eq. (8.30) is –89.673° (–1.5651 radians). For obtaining the correct value of IB, the angle should be corrected as –
θC = 180 + 6 = 180 – 89.673 = 90.327° = 1.5765 radians
and the correct value of IB = 0.2147. Equation (8.29) can be used to compute the vertical stress below rectangular and square footings.
1. Vertical Stress at Any Point P below A Rectangular Footing:
Figure 8.21 shows the plan of a rectangular footing exerting a uniform pressure of intensity q.
The vertical stress at any point P at depth z below the footing shown within the rectangular area can be determined using the following steps:
i. Divide the rectangle ABCD into four smaller rectangles such that point P is the common corner for all these rectangles.
ii. Thus, the smaller rectangles formed are AEPF, EBGP, FPHD, and PGCH.
iii. Determine the Boussinesq influence factors for these rectangles using the corresponding length and width, that is, l1 b1, l2b2, l3b3, and l4b4 at depth z. Let such values obtained be IB1, IB2, IB3, and IB4 for the four rectangles.
iv. The vertical stress at point P at depth z is given by –
σz = (IB1 + IB2 + IB3 + IB4)q …(8.31)
2. Vertical Stress below the Center of a Rectangular or Square Footing:
All rectangles in this case will be of the same size. Hence –
IB1 = IB2 = IB3 = IB4 (say)
Vertical stress at any depth below the center of a rectangular footing is –
σz = 4IBq …(8.32)
3. Vertical Stress at Point P outside the Loaded Area:
Figure 8.23 shows a plan of a uniformly loaded rectangular area ABCD and the vertical stress is required at point P outside the loaded area.
In this case, consider the following rectangles, all of which have a common corner at P:
i. Rectangle 1 – EBHP (IB1), considering (l + le) and b1.
ii. Rectangle 2 – PHCF (IB2), considering (l + le) and b2.
iii. Rectangle 3 – PGDF (IB3), considering le and b2.
iv. Rectangle 4 – EAGP (IM), considering le and b1.
The vertical stress at point P at depth z can be obtained from –
σz = (IB1 + IB2 – IB3 – IB4)q …(8.33)
4. Vertical Stress at a Point Completely Outside the Loaded Area:
Figure 8.24 shows a point that is completely outside the uniformly loaded rectangular area, exerting a pressure q.
In this case, consider the following rectangles, all of which have a common corner at point P:
i. Rectangle 1 – EPHB (IB1), considering (l + le) and (b + be).
ii. Rectangle 2 – EPGA (lB2), considering le and (b + be).
iii. Rectangle 3 – FPHC (IB3), considering (l + le) and be.
iv. Rectangle 4 – FPGD (IB4), considering le and be.
The vertical stress at any depth z below point P is given by –
σz = (IB1 – IB2 – IB3 + IB4)q …(8.34)
5. Vertical Stress Distribution below A Square Footing:
Figure 8.25 shows the vertical stress on a vertical plane below the center of a square footing represented on the x-axis as a function of z/b on the y-axis. It may be observed that the vertical stress increases rapidly from a small value of 0.18 q at z/b = 0.05 to a maximum value of about 0.87q at z/b = 0.323. The vertical stress then decreases rapidly to about 0.5q at z/b = 0.75 and 0.2q at z/b = 1.4. It then decreases gradually to 0.1 q at z/b = 2.
The vertical stress distribution on a vertical plane below the edge of a square footing is shown in Fig. 8.26. It may be observed that vertical stress below the edge is significantly less than that below the center at any depth.
6. Vertical Stress Distribution on a Horizontal below A Square Footing:
The vertical stress below a square footing is maximum at z/b = 0.323. Figure 8.27 shows the vertical stress distribution on a horizontal plane below a square footing at this depth level (z/b = 0.323). The y-axis represents the vertical stress and the x-axis represents the distance from the center of the footing as a product of the width of the footing.
It may be observed that the vertical stress is maximum at the center, with a value of 0.847q, and decreases with distance away from the center toward the edges on either side. The vertical stress is 0.37q below the edge of the footing, which is about 42% of the stress below the center.
Table 8.2 presents the Boussinesq influence factors for vertical stress below the corner of a uniformly loaded rectangular area. IB values are provided for m and n values, starting with m = 0.2 and n = 0.2. These values indicate a depth of five times the width of the footing, and hence, values for m = n < 0.2 are not important as the vertical stress at this depth level is negligible, m and n are in the same ratio as the width and the length of the footing.
Since lengths more than four times the width are uncommon, values in Table 8.2 are provided for m and n up to 4:1. Also, the value of JB initially increases with the increase in m or n, and more or less becomes constant at higher values of m and n. For example, for m = 2, the value of IB increases with the increase in n up to n = 5.6 and thereafter becomes constant. It may be seen that IB = 0.2498 for m = n = 10 and is 0.2499 for m = 10 and n = 20 and 0.2500 for m = n = 20.