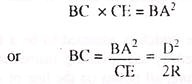Curvature and Refraction in Levelling | Surveying

For long sights and accurate levelling work, the effects of curvature of the earth and refraction of the line of sight shall have to be taken into consideration. Due to curvature, the points appear to be lower than they actually are; while due to refraction, they appear to be higher than they actually are. The effect of curvature being greater than that of refraction, the combined effect causes the points to appear to be lower than they actually are.

Curvature:

Earth has a curved face which is assumed to be a level surface but the line of sight as furnished by the levelling instrument is horizontal and not the level line. Therefore, all points on the line of sight are not equidistant from the surface of the earth and consequently the points read on the staff are not strictly at the same level as horizontal hair of the diagram.

The level line falls away from the horizontal line of sight and the vertical distance between the horizontal line and the level line denotes the effect of curvature of the earth.

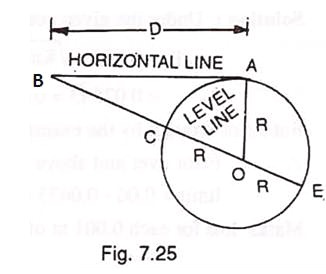
In Fig., 7.24. A’ is the instrument station and P the point where the staff is held. On looking through the telescope, we sight along AB, the horizontal line of sight, and take the staff reading PB. The point B is consider to be at the same level as A, but actually the points C and A are at the same level. The true reading is, therefore, PC.

The difference BC between the observed and true staff readings denotes the error due to curvature of the earth, which may be determined as follows:

In fig 7.25,

D= the length of the sight or the distance from the instruments to the staff station in kilometers

BC= he error due to curvature.

O= the center of the earth.

R= the radius of the earth.

By Geometry, BC x BE =BA²

Or BC (BC= CE) = BC²

Or BC² +BC x CE=BA²

Since BC is usually very small as compared with the diameter of the earth and its square will still be much smaller and may therefore be neglected in calculation:

taxing diameter of the earth as 12,742 kilometers ,we get: 

 

Hence the error in staff reading due to curvature of the earth = 0.0785 D² metres, where D is the distance from the level to the staff in kilometres. The effect of curvature is to increase the staff reading i.e., this error is positive and so the correction is negative.

True staff reading = observed staff reading – 0.0785 D²

Refraction:

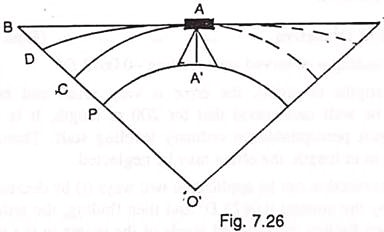
It is a well-established law of physics that rays of light passing through layers of different densities do not remain straight but are refracted or bent down towards the denser medium. Consequently, the ray of light from the staff to the instrument is not straight as AB in fig. 7.26 but it follows a curved path AD concave towards the earth as the near the surface of the earth is denser than the upper layers of air.

Under normal atmospheric conditions, arc AD may be taken as circular and of radius seven times that of the earth. The effect of refraction is therefore 1/7th7 the of that of the curvature, but is of opposite nature. Hence the correction for refraction is additive to the staff reading.

The error due to refraction: 

Combined Correction due to Curvature and Refraction:

Since the effect of curvature is to increase the staff readings and that of refraction is to decrease them and also the effect of curvature is greater than that of refraction, the combined effect is therefore, to increase the staff readings, hence the combined correction is subtractive.

The combined error due to curvature and refraction: 

And true staff reading = observed staff reading -0.0673 D²

For ordinary lengths of sights, the error is very small and hence negligible. It may be well understood that for 200 m length, it is only 0.003 m and it is just perceptible on ordinary levelling staff. Therefore sights less than 200 m in length, the effect may be neglected.

The combined correction can be application two ways:

(i) By decreasing each staff reading by the amount 0.0673 D² and then finding, the reduced levels and

(ii) By first finding the reduced levels of the points in the usual way and then increasing them by the amount 0.0673 D².

The error due to curvature and refraction can be eliminated by equalising back sight and fore sight distances and also by the method of reciprocal levelling which is explained in the article.