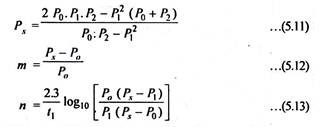Forecasting of Population: 9 Methods | Water Quantity | Water Engineering

The following are the standard methods by which the forecasting of population is done: 1. Arithmetical Increase Method. 2. Geometrical Increase Method. 3. Incremental Increase Method 4. Decreasing Rate Method 5. Simple Graphical Method 6. Comparative Graphical Method 7. Master Plan Method 8. The Logistic Curve Method 9. The Apportionment Method.

1. Arithmetical Increase Method:

This method is based on the assumption that the population is increasing at a constant rate. The rate of change of population with time is constant.

i.e. dp/dt = C (a constant)

integrating P₂-P₁ = C(t₂-t₁)……………..(5.5)

Where P₁ = Population at the time t₁ first census

P₂ = Population at the time t₂ last available census

The value of constant C is determined.

Now the population after n decade can be determined by the formula

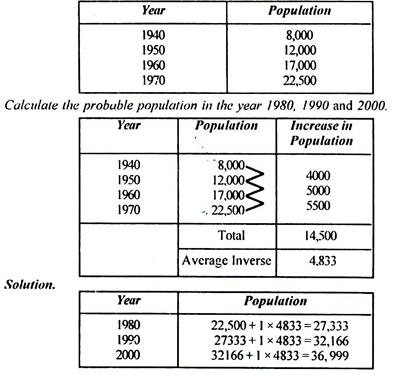
P_n = P + n. C

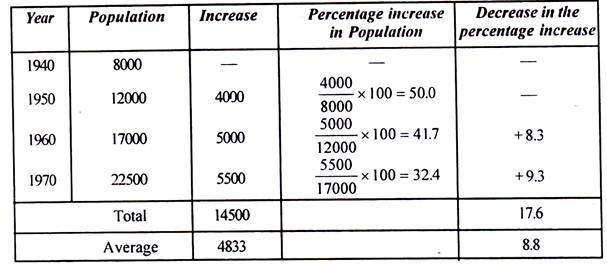
Example 1:

The following data have been noted from the census department:

2. Geometrical Increase Method:

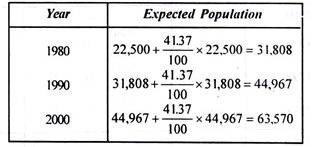
This method is based on the assumption that the percentage increase in population from decade to decade remains constant. In this method the average percentage of growth of last few decades is determined; the population forecasting is done on the basis that percentage increase per decade will be the same.

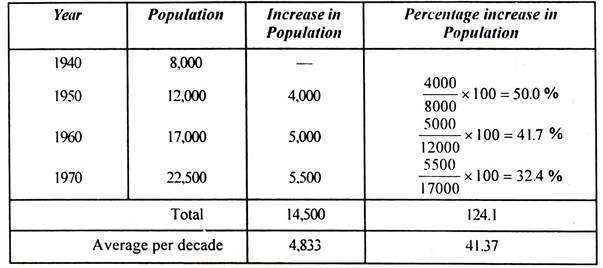
If the present population is P and the average percentage growth is I_G the population at the end of n decade will be:

Example 2:

Forecast the population of example 1 by means of geometrical increase method.

The population at the end of various decades shall be as follows:

3. Incremental Increase Method:

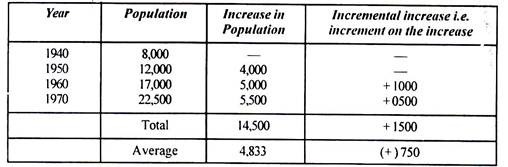
This method is improvement over the above two methods. The average increase in the population is determined by the arithmetical method and to this is added the average of the net incremental increase once for each future decade.

P is the present population, la = Average Arithmetical increase, and l_C is the average incremental increase, then population after ‘n’ decade will be

Pn = P + n (la + Ic)

Solved example 3 will explain this method clearly.

Example 3:

Forecast the population of example 1, by means of incremental increase method.

Solution:

The population at the end of various decades shall be as follows:

In the year 1980,

P₁₉₈₀= 22,500 +1 x (4833 + 750)

P₁₉₈₀ = 28,083

P₁₉₉₀ =28,083+ (4833 +750) x 1

P₁₉₉₀ = 33,666

and P₂₀₀₀ =33,666+(4833+ 750)

P₂₀₀₀ = 39249

4. Decrease Rate of Growth Method or Decreasing Rate Method:

It has been seen that all life grow within limited space. If the complete growth of a very old city is plotted, it will be seen that the curve has S-shape, which indicates that early growth takes place at an increasing rate, latter growth is at a decreasing rate which indicates that saturation limit is reached.

In this method, the average decrease in the percentage increase is worked out and is then subtracted from the latest percentage increase for each successive decade.

Example 4:

Solve example 1, by using decrease rate of growth method.

Solution:

Now the population at the end of various decades shall be as follows:

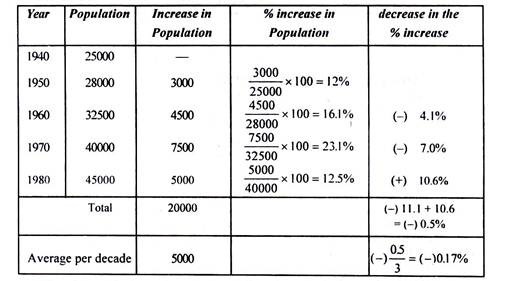
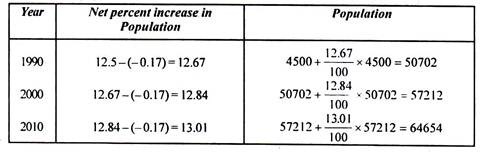
Example 5:

The population of five decades from 1940 to 1980 are given below. Find out the population in decades 1990, 2000 and 2010 by using decrease rate of growth method.

Solution:

Now the population at the end of various decades shall be as follows:

5. Simple Graphical Method:

In this method the populations of last few decades are correctly plotted to a suitable scale on the graph with respect to decade. The curve is smoothly extended to forecast the future population. The graph of present city is plotted from the beginning and it will show the growth curve. Fig. 5.1 shows the typical growth curve of a city of example 1.

After extending the curve and determining the forecasts of population at various decades, following results are noted on the graph of Fig 5.1.

6. Comparative Graphical Method:

In this method, the cities having conditions and characteristics similar to the city whose future population is to be estimated are first of all selected. It is then assumed that the city under consideration will develop as the selected similar cities have developed in the past. This method has a logical background, and if statistics of development of similar cities are available quite precise and reliable results can be obtained.

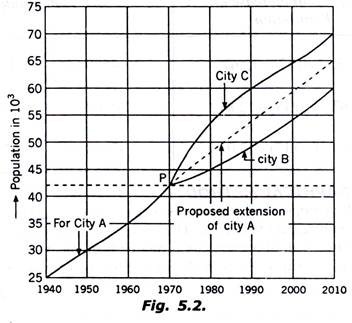
Consider Fig. 5.2. Let the population of a city A be given for 4 decades (say 1940, 1950, 1960 and 1970) the population time curve is then plotted.

Now, Suppose it is required to estimate the population of the city A at the end of year 2010. And let the available data show that this city A has reached the present population of 42500 in the year 1970. Then the available data of similar cities Band C is analyzed. Let it be found that city B has reached 42500 in the year 1940 then its curve is plotted beyond the year 1940 onward.

However, this curve for city B should start from point P which represents the present population of city A. Similarly, the population of city C is plotted from the year it has reached 42500 onwards. Now the curve for city A is carefully extended between the curves of cities B and C as shown in Fig. 5.2.

Fig. 5.2 shows the development of cities A,B, C and D. The development of the city ‘X’ under consideration has been shown by dotted line. Future expected population at any decade can be directly determined from this graph.

7. The Master Plan Method or Zoning Method:

The development of towns and cities is not allowed in haphazard way. For the development of the towns and cities, their master plans are prepared. The city is divided into various zones such as commercial centres, industrial areas, residential areas, the schools, colleges, parks etc. The future expansion of the cities is strictly regulated by various by­laws of corporations and other local bodies, according to the master plan.

The master plans are prepared for the development of the cities for 25-30 years. The population densities for various zones of the towns to be developed are also fixed. Now when the population of a particular zone is fixed, it is very easy to design the water supply schemes for the particular zones. The future development of the water works is also designed on the basis of the master plan.

Table 5.5 gives the common population densities for preparation of master plans:

8. Logistic Curve Method:

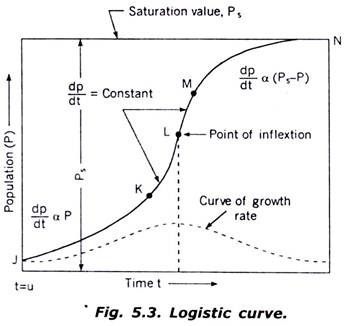
If the population of a town is plotted with respect to time, the curve so obtained under normal conditions shall be as shown in Fig. 5.3.

The early growth of the city is shown by curve JK at an increasing rate of dp/dt α p. The growth rate between point K to M follows curve of dp/dt = constant. The transitional curve KM also passes through the point of inflexion L.Later on the growth from M to N follows the decreasing rate i.e., dp/dt α (p_s-p) where p is population of the town at point t from the origin j and p_s is the saturation value of the population. The s-shaped curve JKLMN is called logistic curve.

P.F. Verhulst after long research work has given the following mathematical solution of logistic curve:

McLean further suggested that if three pairs of the characteristics values P₀, P₁ and P₂ at times t₀, t₁, and t₂ which are extending over the useful range of the population are so chosen that t_o= 0, t₁, and t₂ = 2t₁ the saturation values P_s and constants m and n can be determined from the following equation:

Example 6:

Following is the population of a city as noted from the census department:

Determine (a) the saturation population (b) the expected population in 1980 and the equation of logistic curve.

Solution:

(b) Now substituting the values of P_s m and n in equation (5.10),

9. The Apportionment Method:

This is also known as the ratio method of forecasting future population. In this method the census population record is expressed as the percentage of the population of the whole country. The population of the city under consideration and the country’s population for the last four to five decades are collected from the census department.

The ratio of the town under consideration to the national population is calculated for these decades. Now a graph is plotted between these ratios and the time. The extension of this graph will give the ratio corresponding to the future years for which the forecasting of population is to be done.

The ratio so obtained is multiplied by the expected national population at the end of the designed period, for determining the expected national population of the town under reference.

This method is suitable for those towns and cities whose development is likely to take place according to the national growth.